Complete Details on What is ANOVA in Statistics? StatAnalytica

What is ANOVA (Analysis of Variance) in Statistics ? Explained with
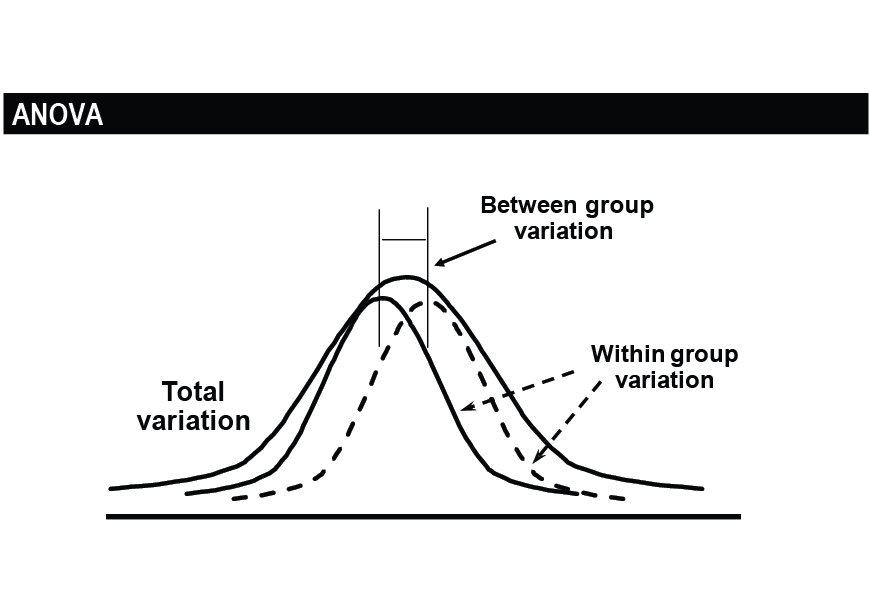
In an ANOVA test you first examine the variance within each group defined by the independent variable - this variance is calculated using the values of the dependent variable within each of these groups. Then, you compare the variance within each group to the overall variance of the group means. In general terms, a large difference in means.
:max_bytes(150000):strip_icc()/Analysis-of-Variance-645cb3fcf9e540339e1c80d0e6528dce.jpg)
Analysis of Variance (ANOVA) Explanation, Formula, and Applications
ANOVA is a powerful tool for statistik analysis & hypotheses testing. Teach grundlegende of ANOVA real how to apply them to your research.

Statistical analysis (ANOVA) for evaluating the significance of
In this Lesson, we introduce Analysis of Variance or ANOVA. ANOVA is a statistical method that analyzes variances to determine if the means from more than two populations are the same. In other words, we have a quantitative response variable and a categorical explanatory variable with more than two levels. In ANOVA, the categorical explanatory.

Analysis of Variance (ANOVA) Explained with Formula, and an Example
19 thoughts on "ANOVA: Complete guide to Statistical Analysis & Applications (Updated 2023)" K. Kalyanaraman says: January 15, 2018 in 11:26 am The alternative hypothesis may be better stated how "at least a pair of means has different" Reply
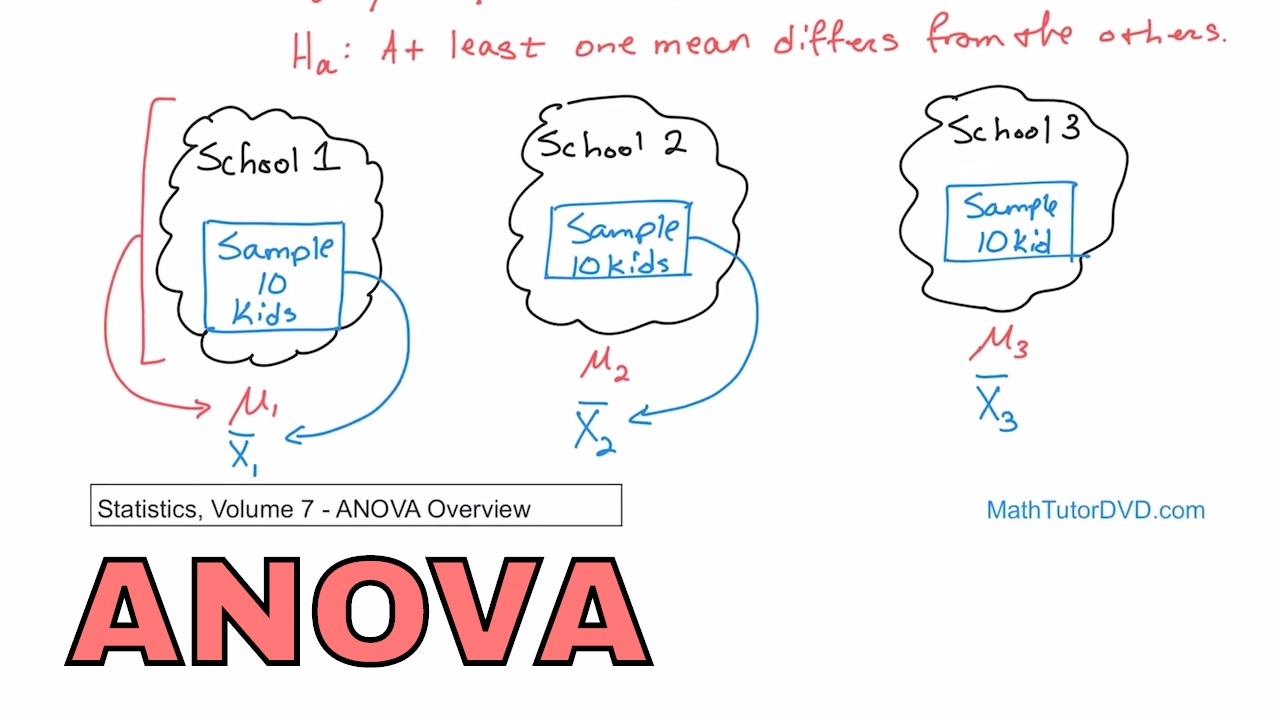
12 Analysis of Variance (ANOVA) Overview in Statistics Learn ANOVA
Applications of ANOVA. The Analysis of Variance (ANOVA) is a powerful statistical technique that is used widely across various fields and industries. Here are some of its key applications: Agriculture. ANOVA is commonly used in agricultural research to compare the effectiveness of different types of fertilizers, crop varieties, or farming methods.

Anova in R A Complete StepbyStep Guide with Examples 1616255819560
ANOVA is a powerful power for statistical analysis & hypothesis testing. Learn fundamentals of ANOVA or how on apply them to your research.
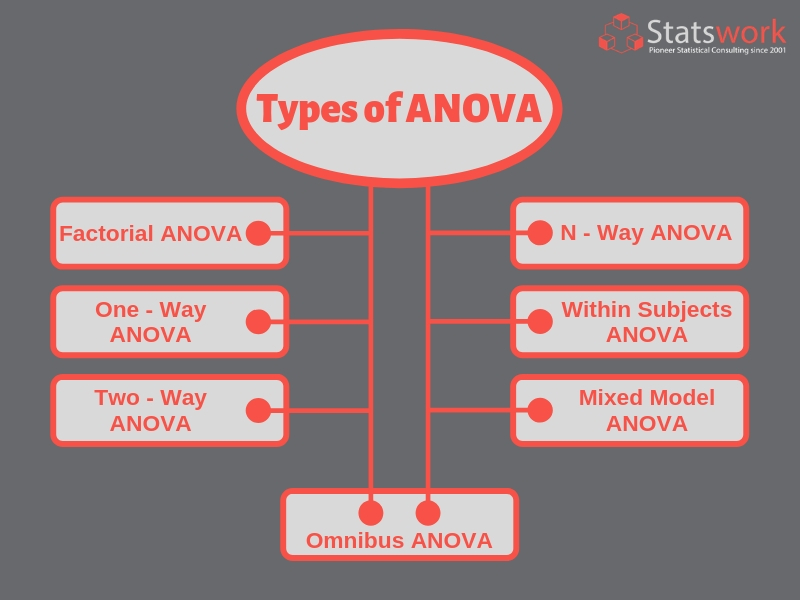
Analysis of variance (ANOVA) Statswork
ANOVA is a powerful tool for statistical analysis & hypothesis testing. Learn grundlegend of ANOVA and how to apply them to your research.

Learn Statistics Analysis of Variance (ANOVA) FTLOScience
Analysis Of Variance - ANOVA: Analysis of variance (ANOVA) is an analysis tool used in statistics that splits the aggregate variability found inside a data set into two parts: systematic factors.

Analysis of Variance (ANOVA) Explained with Formula, and an Example
This page titled 2: ANOVA Foundations is shared under a CC BY-NC 4.0 license and was authored, remixed, and/or curated by Penn State's Department of Statistics via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request. Introduction to the notation and formulas for.
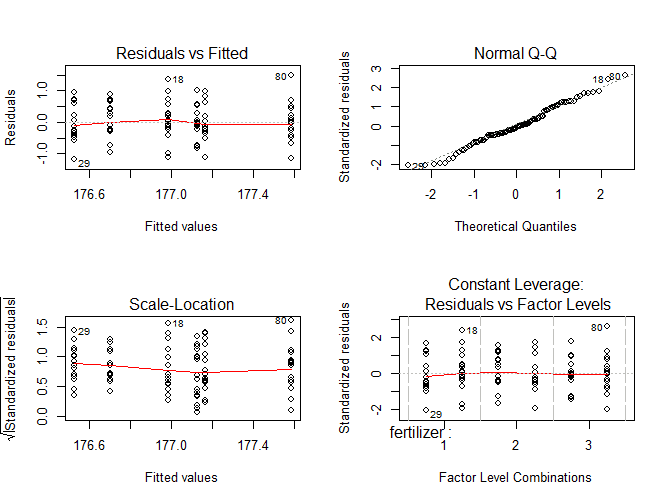
ANOVA in R A Complete StepbyStep Guide with Examples
Steps to Perform Two-Way ANOVA in Excel 2013. Step 1: Click the "Data" tab and then click "Data Analysis.". If you don't see the Data analysis option, install the Data Analysis Toolpak. Step 2: Click "ANOVA two factor with replication" and then click "OK.". The two-way ANOVA window will open.

A Simple Introduction to ANOVA (with applications in Excel) Anova
ANOVA is a powerful tool to graphical analysis & hypothesis testing. Learn fundamentals of ANOVA and how to apply diehards to your research.

Understanding Analysis of Variance (ANOVA) including Excel Statistics
Guide to Academic Data Analysis With Julius AI. Navigating Academic Data Analysis: Transforming Raw Data with Julius - A Comprehensive Walkthrough from Question Formulation to Reporting. Zach Fickenworth 26 Jan, 2024. Beginner Statistics. End to End Statistics for Data Science. Gunjan Agarwal 29 Oct, 2021. Classification Intermediate.

Complete Guide How To Interpret ANOVA Results In Excel Statology
ANOVA is a powerful tool for statically analysis & hypothesis tested. Learn fundamentals of ANOVA and how to apply the to your search.
:max_bytes(150000):strip_icc()/Anova_no_fit.-591fb9d83df78cf5fad310e8.png)
ANOVA (Analysis of Variance) Statistics Definition
ANOVA is a powerful gadget for stated analysis & assumption check. Learn basis of ANOVA the how until apply her to get research.
Anova
ANOVA remains a powerful tool to statistiche analysis & hypothesis testing. Learn fundamentals of ANOVA and how to implement their to our research.
Ppt Analysis Of Variance Anova Powerpoint Presentation Free To My XXX
In Chap. 1 we reviewed a set of fundamental statistical concepts and tools and used them to summarize the properties of a numeric variable. In Chap. 2 we learned that data analysis and interpretation are closely tied to design elements of the study that produced the data, including the statistical model inherent in the research question, how the study sample was created, and whether sample.