P Value Definition, Formula, Table, Finding Pvalue, Significance

Pvalue Formula What is Pvalue Formula?, Examples

The p-value 0.03 means that there's 3% (probability in percentage) that the result is due to chance — which is not true. People often want to have a definite answer (including me), and this is how I got myself confused for a long time to interpret p-values. A p-value doesn't *prove* anything.

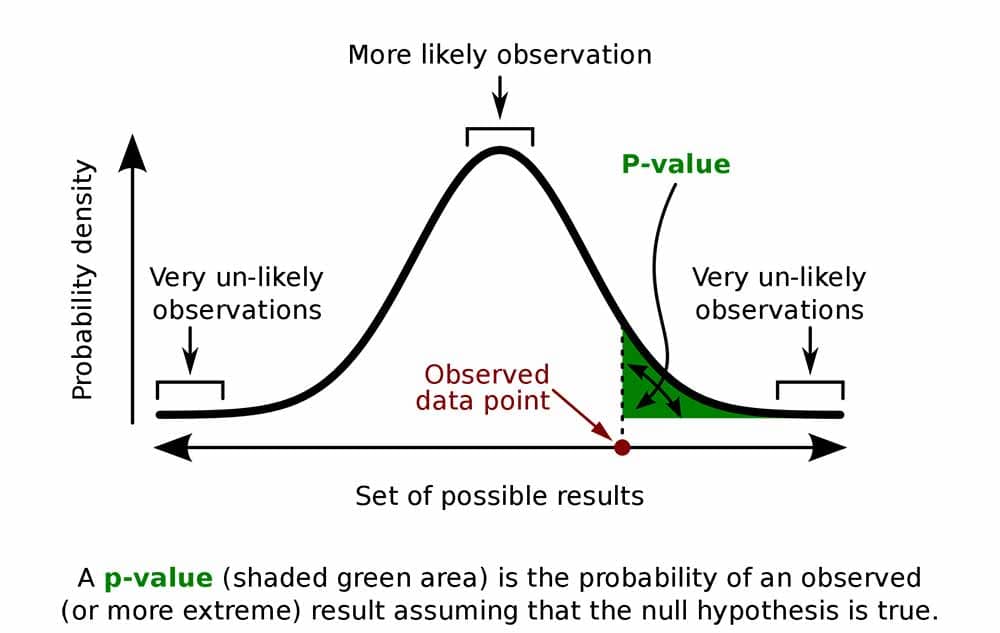
Understanding PValues and Statistical Significance

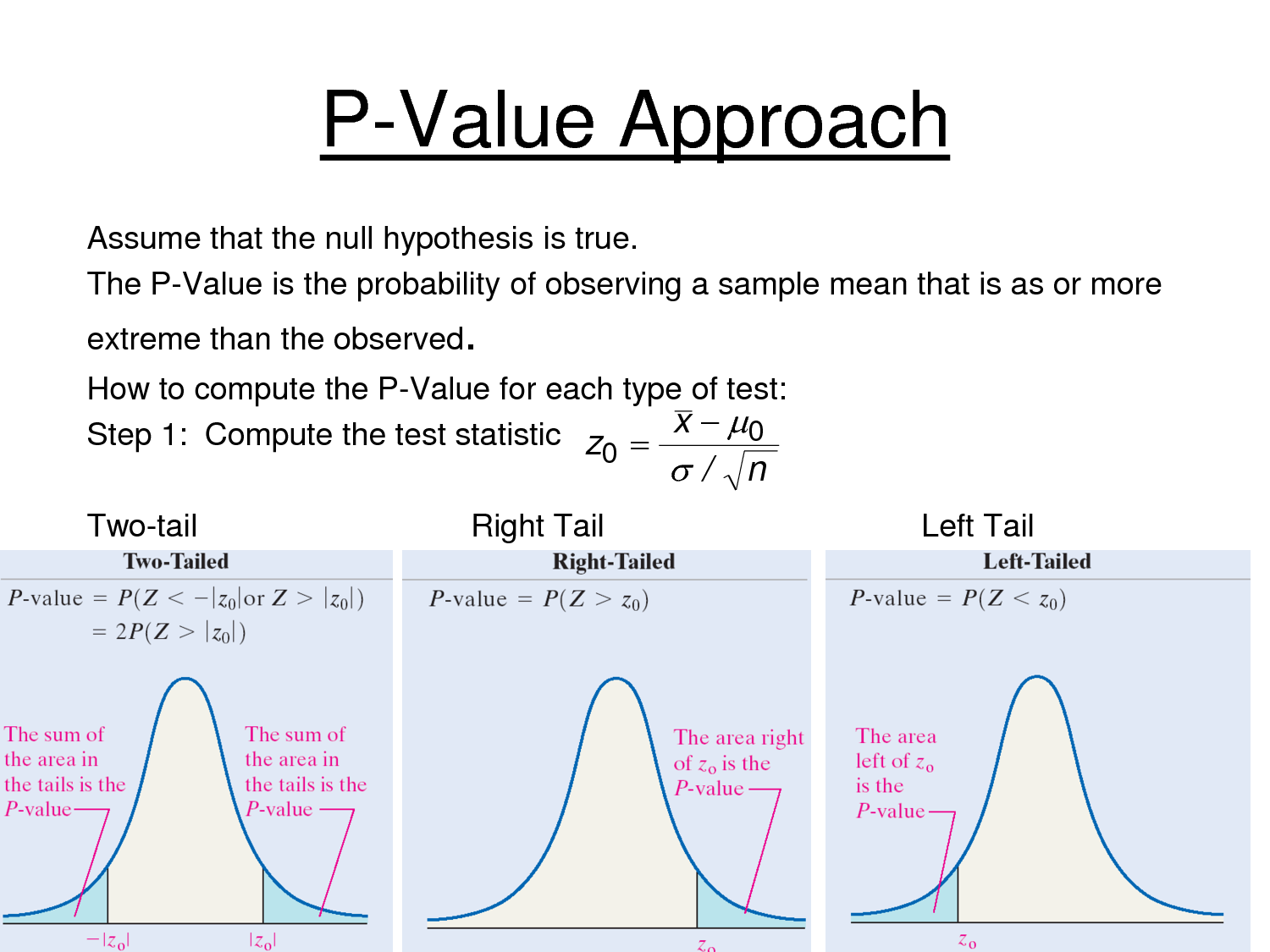
The calculated p-value is used in comparison with a predefined significance level (alpha) to make decisions about the null hypothesis. If the p-value is less than or equal to alpha, typically 0.05, the results are considered statistically significant, leading to the rejection of the null hypothesis in favor of the alternative hypothesis. If the.

PValue What It Is, How to Calculate It, and Why It Matters

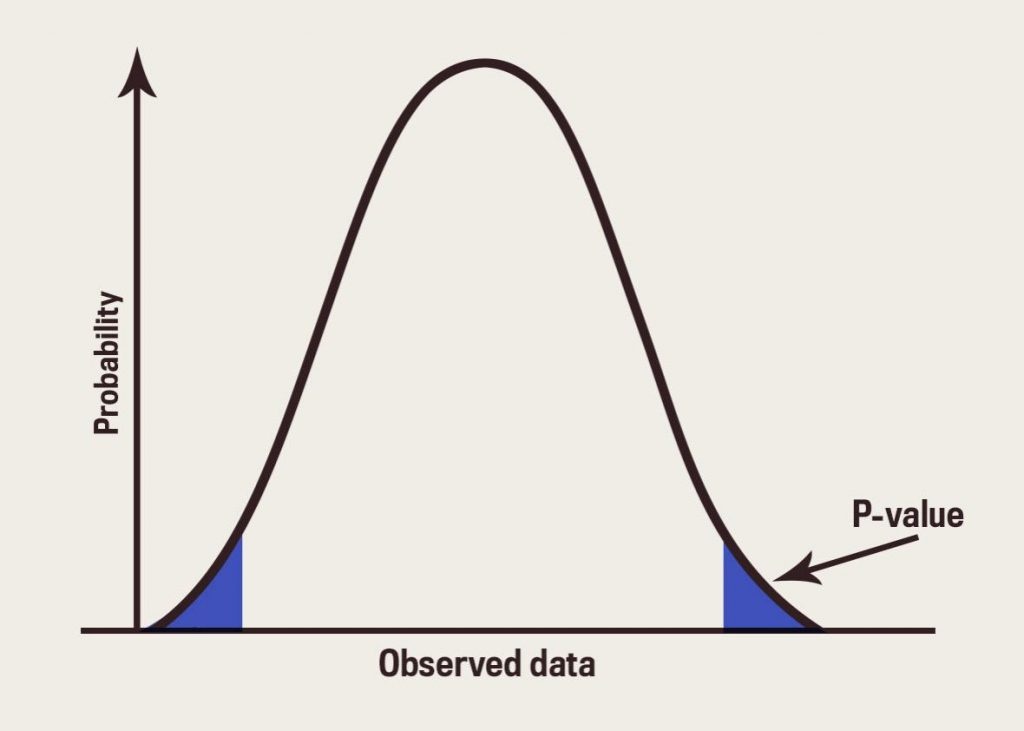
The p value gets smaller as the test statistic calculated from your data gets further away from the range of test statistics predicted by the null hypothesis. The p value is a proportion: if your p value is 0.05, that means that 5% of the time you would see a test statistic at least as extreme as the one you found if the null hypothesis was true.

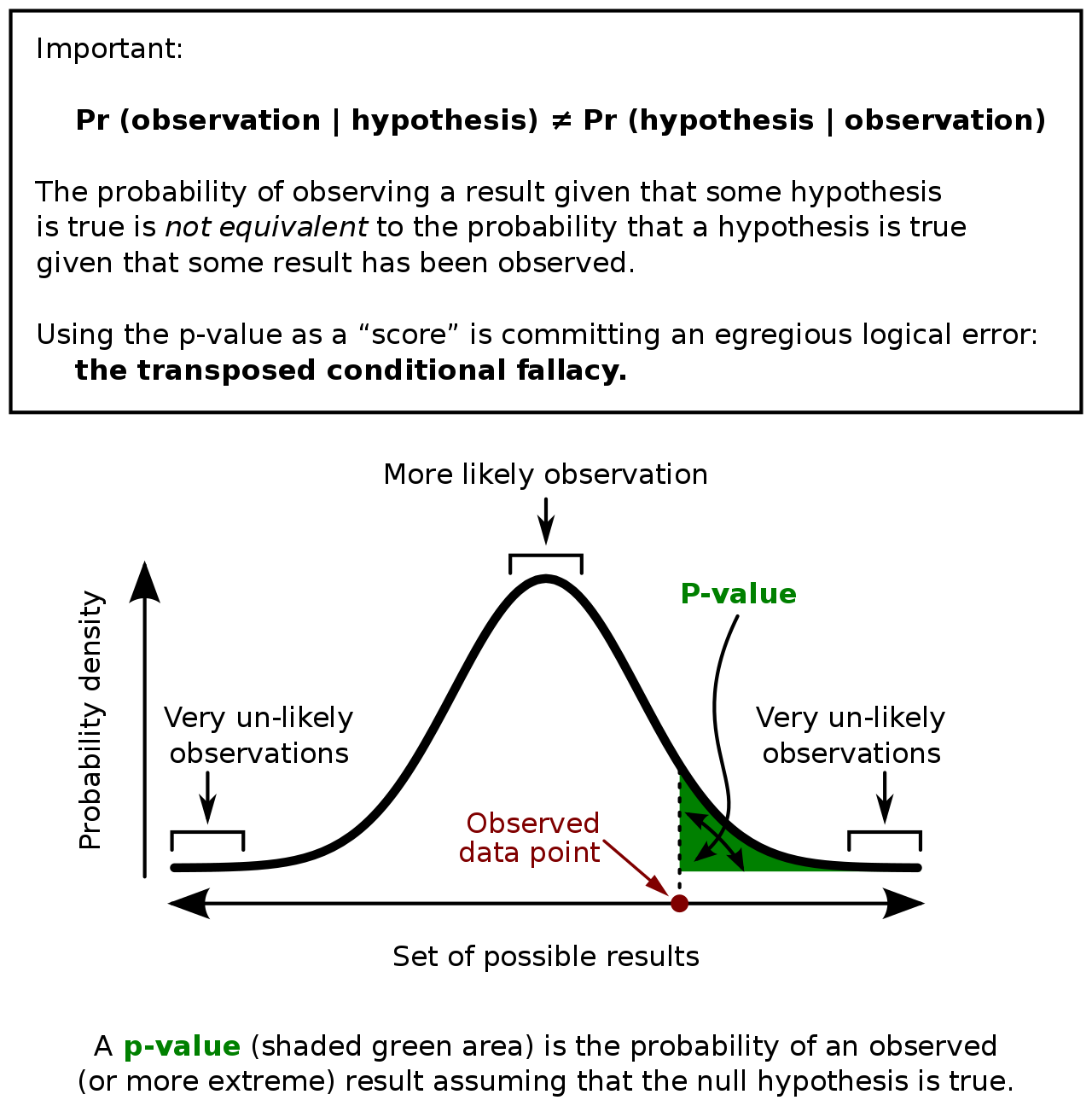
PValue Mathematical Mysteries

The p value determines statistical significance. An extremely low p value indicates high statistical significance, while a high p value means low or no statistical significance. Example: Hypothesis testing. To test your hypothesis, you first collect data from two groups. The experimental group actively smiles, while the control group does not.

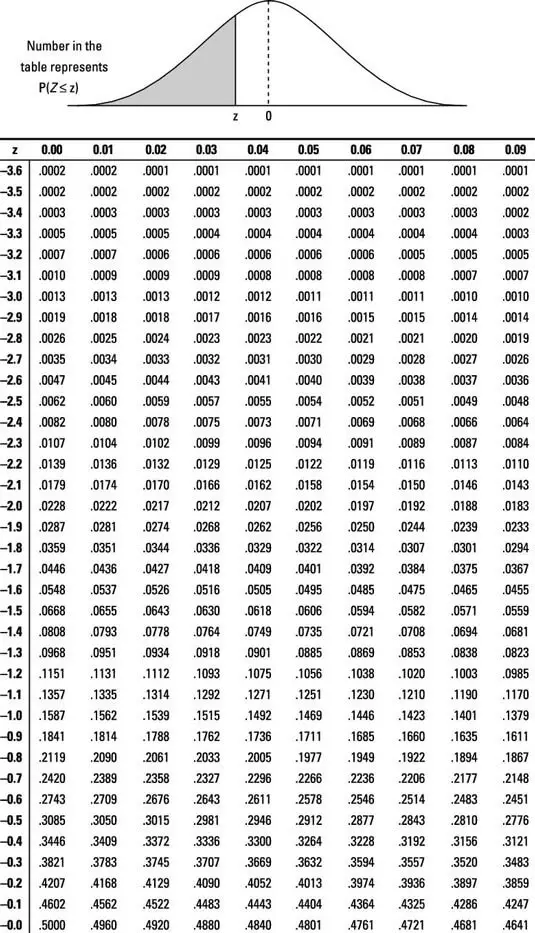
Pvalue Definition, Significance, Formula, Table, Finding Pvalue

P-Value: The p-value is the level of marginal significance within a statistical hypothesis test representing the probability of the occurrence of a given event. The p-value is used as an.

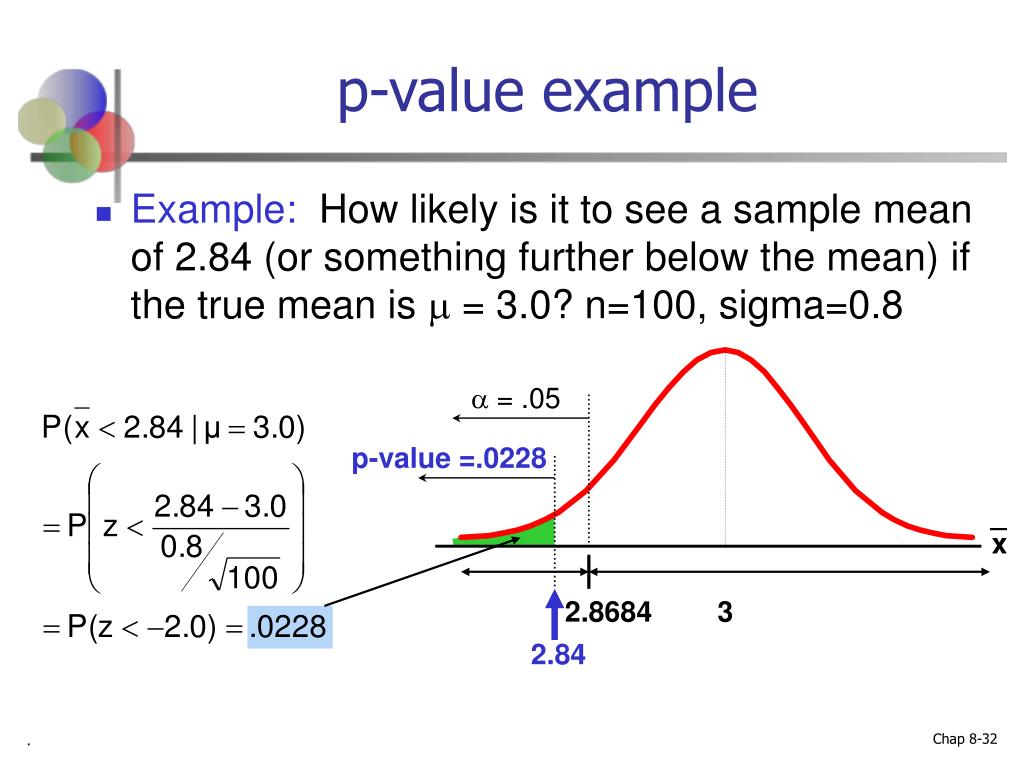
PPT Chapter 8 Introduction to Hypothesis Testing PowerPoint

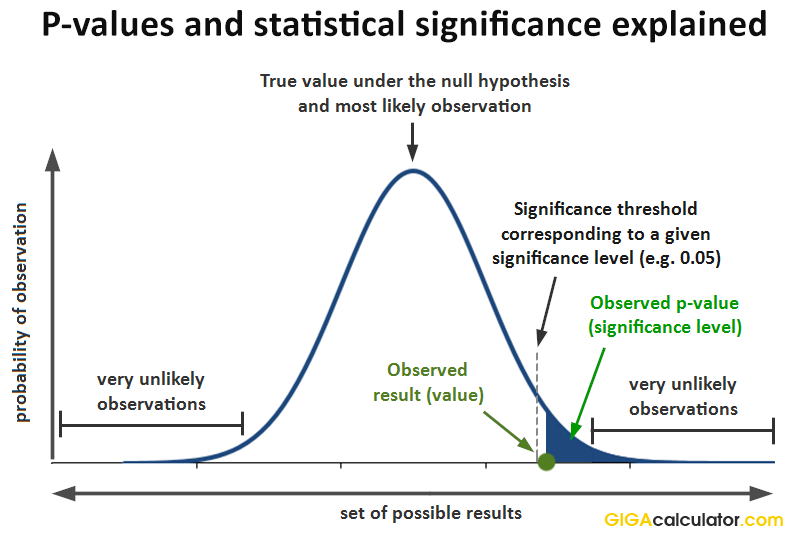
A p-value, or probability value, is a number describing how likely it is that your data would have occurred by random chance (i.e., that the null hypothesis is true). The level of statistical significance is often expressed as a p-value between 0 and 1. The smaller the p -value, the less likely the results occurred by random chance, and the.

Pvalue

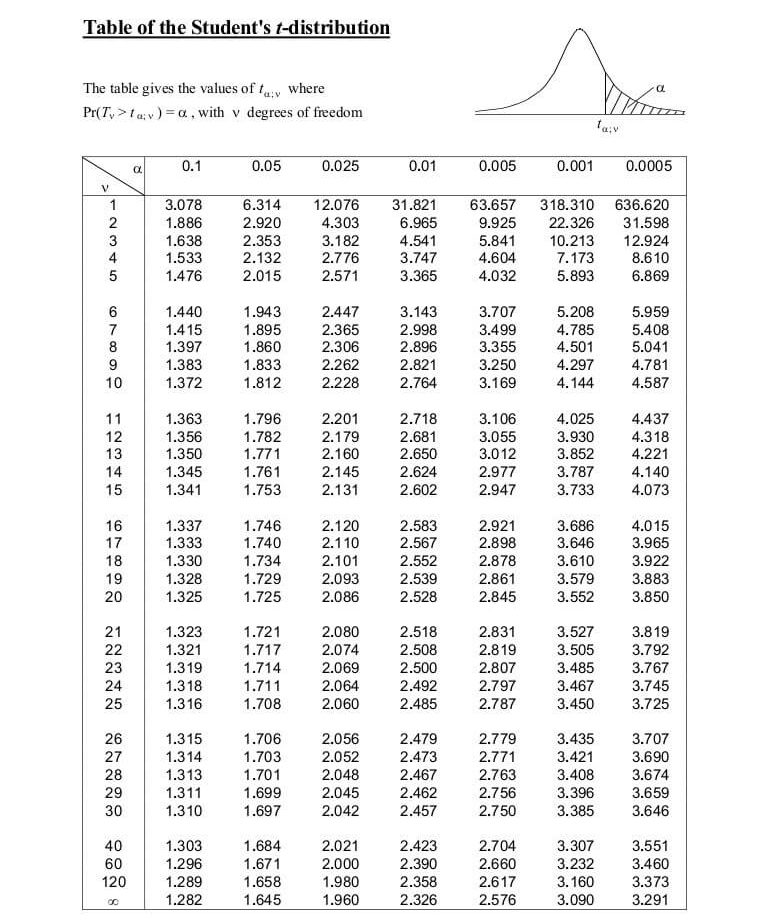
The P-value for conducting the left-tailed test H 0: μ = 3 versus H A: μ < 3 is the probability that we would observe a test statistic less than t* = -2.5 if the population mean μ really were 3. The P-value is therefore the area under a t n - 1 = t 14 curve and to the left of the test statistic t* = -2.5.

How to calculate pvalues YouTube

p-value interpretation in outcomes of experiments. When a p-value is calculated for the outcome of a randomized controlled experiment, it is used to assess the strength of evidence against a null hypothesis of interest, such as that a given intervention does not have a positive effect. If H 0: μ 0 ≤ 0% and the observed effect is μ 1 = 30% and the calculated p-value is 0.025, this can be.

P Value Definition, Formula, Table, Finding Pvalue, Significance

It does not measure support for the alternative hypothesis. This limitation leads us into the next section to cover a very common misinterpretation of P values. P Values Are NOT the Probability of Making a Mistake. Incorrect interpretations of P values are very common. The most common mistake is to interpret a P value as the probability of.

P Value Definition, Formula, Table, Finding Pvalue, Significance

The p-value is the probability of the observed data given that the null hypothesis is true, which is a probability that measures the consistency between the data and the hypothesis being tested if, and only if, the statistical model used to compute the p-value is correct ( 9 ). The smaller the p-value the greater the discrepancy: "If p is.

Hypothesis testing tutorial using p value method Prwatech

P-value if the CTR of new version is higher than current version with a result of 15.0. As we can see, p value is much smaller than the previous one. Assume the p value is now 0.02. Thus, according to the confidence level of 95%, this p value indicates the results are statistically significant.

What is P Value How to interpret and calculate P Value YouTube

A high P-value, between 0.5 and 1.0, means that it is more likely that the results occurred by random chance, or that the difference is not statistically significant in the case of a hypothesis test.

Understanding PValues and Statistical Significance

The height coefficient in the regression equation is 106.5. This coefficient represents the mean increase of weight in kilograms for every additional one meter in height. If your height increases by 1 meter, the average weight increases by 106.5 kilograms. The regression line on the graph visually displays the same information.

The p value definition and interpretation of pvalues in statistics

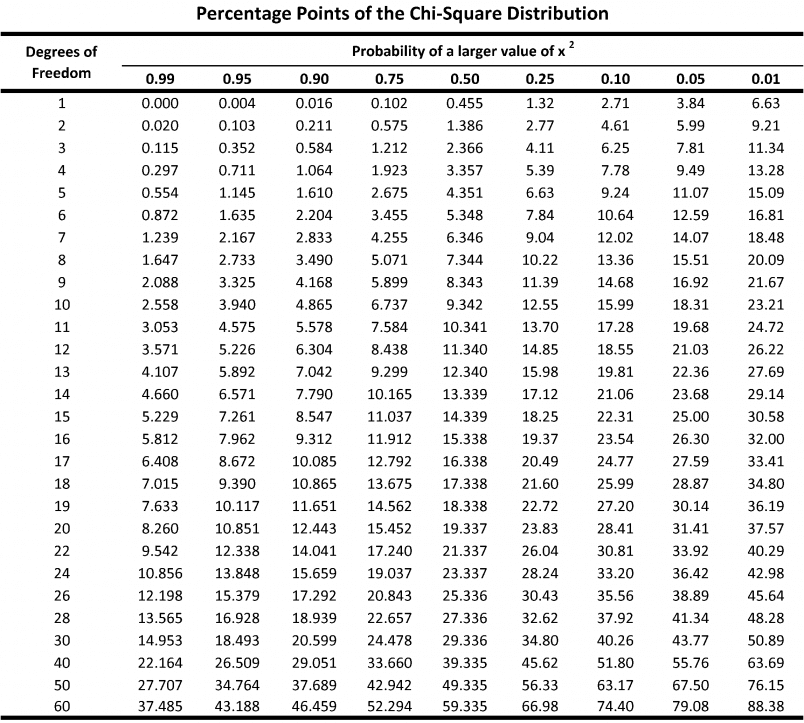
Assuming that the null hypothesis is true, and p = 0.25, the sampling distribution of sample proportion with n = 60 should be approximately normal, with a mean = p = 0.25 and standard deviation of √((p·(1-p))/n) ≈ 0.056. So a sample with p-hat = 0.3 should only have a z-score ≈ 0.89, and there should be ≈ 0.187 probability of getting a.

pvalue Lean Manufacturing and Six Sigma Definitions

These are as follows: if the P value is 0.05, the null hypothesis has a 5% chance of being true; a nonsignificant P value means that (for example) there is no difference between groups; a statistically significant finding (P is below a predetermined threshold) is clinically important; studies that yield P values on opposite sides of 0.05.

PPT Understanding Pvalues and Confidence Intervals PowerPoint

In null-hypothesis significance testing, the -value [note 1] is the probability of obtaining test results at least as extreme as the result actually observed, under the assumption that the null hypothesis is correct. [2] [3] A very small p -value means that such an extreme observed outcome would be very unlikely under the null hypothesis.